MOONSUN
[알고리즘] 슬라이딩 윈도우 & 단조 큐 : 구간을 효율적으로 관리 본문
데이터를 분석하거나 문제를 풀 때, 연속된 구간의 합을 빠르게 구하는 게 핵심인 경우가 많다.
하지만, 배열 크기가 크고, 구간 합을 여러 번 계산해야 하면, 매번 전체 합을 계산하면 시간이 많이 걸리는 문제가 있다.
그래서 1.중복 계산을 제거하거나, 2.효율적으로 구간을 처리를 하는 방법이 필요하다.
이번 글에서는 2. 효율적으로 구간을 처리 하는 방법 2가지(슬라이딩 윈도우, 단조 큐)를 알아보고자 한다.
1. 슬라이딩 윈도우 (Sliding Window)
투 포인터의 일종으로 start와 end 로 표현되는 연속된 구간(윈도우)를 한 칸씩 옮겨가며 문제를 해결한다.
- 이때 윈도우의 크기는 고정 또는 가변 일수 있다.
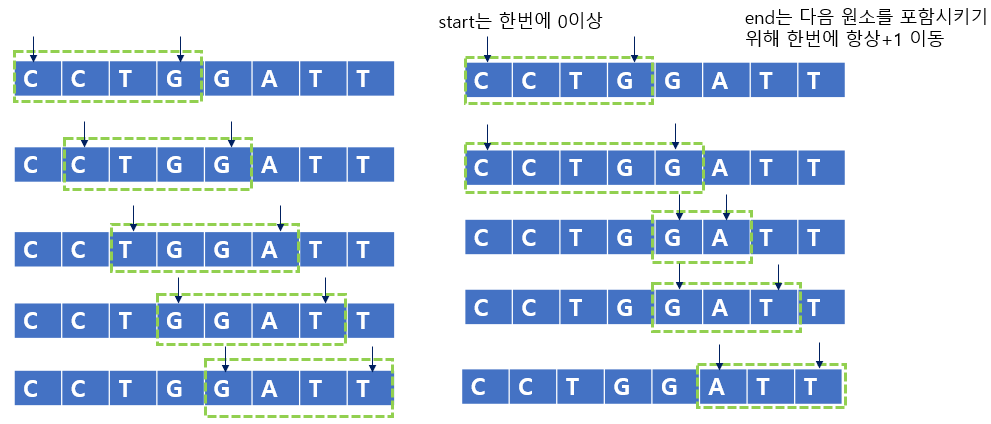
슬라이딩 윈도우의 구간 정보를 관리하는 도구로 단조 큐를 사용할 수 있다.
2. 단조 큐 (Monotonic Queue)
모노톤(monotone)의 뜻 : 단조(單調)
- 단조 증가: 값이 계속 같거나 커짐
- 단조 감소: 값이 계속 같거나 작아짐
단조 큐는 큐 안의 원소를 항상 단조 상태로 유지 하는 자료구조
2-1. 특징
- 일반 큐처럼 들어온 순서대로 쌓지 않음
- 새 값이 들어올 때, 미래에 최소/최대가 될 수 없는 값은 제거
- 앞/뒤 추가·삭제 최적화를 위해 deque 사용
2-2. 삽입 과정
- 새 값이 들어오면 뒤에서부터 자기보다 큰 값 제거(pop_back)
- 새 값 push_back
- 윈도우 최소값 = deque의 front
2-3. 시간복잡도 관점
- 새 값을 넣을 때 뒤에서 불필요한 값들을 한꺼번에 제거 하므로, 겉으로는 연산이 많아 보이지만,
- 각 원소는 최대 1번만 덱에서 제거되기 때문에
- 전체 배열에 대해 수행되는 연산은 원소 개수 N에 비례 → O(N)
즉, 한 번 들어온 원소는 한 번만 제거되므로, 반복 연산이 겉보기보다 많아 보여도 총 연산량은 선형이라는 점
3. 투 포인터(Two Pointer)와 차이점은?
- 투 포인터 = “구간 찾기”
- 슬라이딩 윈도우 / 단조 큐 = “구간 내부 정보를 효율적으로 관리하면서 원하는 값(최소, 최대 등)을 바로 가져오기”
정리: 투 포인터는 구간 위치 탐색에 집중, 슬라이딩 윈도우/단조 큐는 구간 내부 정보 관리에 집중.
| 구분 | 투 포인터 | 슬라이딩 윈도우 / 단조 큐 |
| 목적 | 조건을 만족하는 구간 위치 찾기 | 구간 내부 값(합, 최소, 최대)을 빠르게 계산 |
| 포커스 | 구간의 시작/끝 | 구간 안 값 관리 |
| 구현 | 포인터 2개 | 포인터 + deque(또는 기타 자료구조) |
| 예시 | 합이 N인 연속 구간 | 구간 최소값, 최대값, 이동 평균, 그래픽 밝기 표현 |
4. 정리
- 슬라이딩 윈도우 : 구간을 옮겨가며 확인하는 기법 (고정/가변 크기 가능)
- 문제점: 윈도우 최소값/최대값을 빠르게 구하는 게 어려움
- 단조 큐 : 불필요한 값 제거 + 덱으로 단조성 유지 → 윈도우 최소/최대값 O(1)로 확인
최소값/최대값을 빠르게 구하는 게 어려운 슬라이딩 윈도우의 문제점를 극복하기 위해 단조 큐를 활용한다.
5. 슬라이딩 윈도우 + 단조 큐 예시
- 입력 배열: [5, 3, 8, 2, 6]
- 윈도우 크기: 3
- 목표: 각 윈도우의 최소값
5-1. 핵심 규칙
- 새 값 삽입 전 : 덱 뒤에서부터 자신보다 큰 값 제거 → 단조성 유지 (pop_back)
- 새 값 삽입 : 덱 뒤에 삽입 (push_back)
- 윈도우 밖 값 제거 : 덱 앞(front) 인덱스가 현재 윈도우 밖이면 제거 (pop_front)
- 최소값 확인 : 덱 앞(front) 값이 현재 윈도우 최소값
5-2. 단계별 진행
| i (인덱스) | 값 x | 덱 처리 전 | 뒤에서 비교 | 삽입 후 덱 | 윈도우 밖 제거 | 최종 덱 | 윈도우 최소값 |
| 0 | 5 | [] | — | [(5,0)] | — | [(5,0)] | 5 |
| 1 | 3 | [(5,0)] | 5>3 → pop | [(3,1)] | — | [(3,1)] | 3 |
| 2 | 8 | [(3,1)] | 3≤8 → 유지 | [(3,1),(8,2)] | — | [(3,1),(8,2)] | 3 |
| 3 | 2 | [(3,1),(8,2)] | 8>2 pop → 3>2 pop | [(2,3)] | (i-L=0, 5,0 없음) | [(2,3)] | 2 |
| 4 | 6 | [(2,3)] | 2≤6 → 유지 | [(2,3),(6,4)] | (i-L=1, 3,1 없음) | [(2,3),(6,4)] | 2 |
5-3. 정리
- 덱에는 항상 윈도우 안의 후보 최소값들만 남음
- 맨 앞(front) 값이 윈도우 최소값
- 새 값이 들어올 때 뒤에서 큰 값 제거 → 미래에 최소값이 될 수 없는 값 제거
- 윈도우 이동 시, 앞 값이 범위를 벗어나면 제거
덱에는 항상 “현재 윈도우에서 최소값이 될 수 있는 후보들”만 남아 있어서, 최소값 확인이 O(1)로 가능하다.
'CS' 카테고리의 다른 글
| [알고리즘] 효율적인 '분할 정복' 정렬(N log₂N): 퀵 정렬(Quick Sort), 병합 정렬(Merge Sort) (0) | 2025.09.26 |
|---|---|
| [알고리즘] 단순 정렬(N²) : 버블(Bubble Sort), 선택(Selection Sort), 삽입(Insertion Sort) 과 안정/불안정 정렬 (0) | 2025.09.25 |
| [알고리즘] LUT & 투 포인터 : 중복 계산 줄이기 (0) | 2025.09.19 |
| [자료구조] 우선순위 큐(priority queue) 와 힙(Heap) (0) | 2025.09.12 |
| [자료구조] 스택(Stack)&큐(Queue) 와 컨테이너(Container) (0) | 2025.09.11 |
