MOONSUN
[알고리즘] Dynamic Programming(DP:동적 프로그래밍)이란? 본문
복잡해 보이는 문제도 작은 문제로 나누어 효율적으로 해결하는 방법이 있다.
바로 동적 프로그래밍(Dynamic Programming, DP)이다.
DP는 문제를 여러 개의 작은 부분 문제로 분해하고,
이 부분 문제들의 결과를 저장해 재사용함으로써 중복 계산을 제거하는 알고리즘 기법이다.
일반적인 재귀나 완전 탐색으로는 시간 제한을 넘길 수 있는 문제들도, DP를 사용하면 빠르게 해결할 수 있기 때문에 알고리즘 분야에서 매우 중요한 개념이다.
이 글에서는 동적 프로그래밍의 개념에 대해 알아보고, 예시 코드 구현까지 작성해 보도록 하자.
0. Dynamic Programming(DP : 동적 프로그래밍)
동적 프로그래밍(Dynamic Programming, DP)은
큰 문제를 작은 부분 문제(Subproblem)로 나누고,
그 부분 문제의 해답을 저장(메모)해 재활용함으로써,
전체 문제를 효율적으로 해결하는 알고리즘 기법이다.
여기서 “Dynamic(동적)”이라는 단어는 우리가 흔히 알고 있는 정적(static)의 반대 개념과는 조금 다르며,
순차적으로 문제를 전개하는 과정(sequential, time-evolving)을 의미한다.
과거 수학·최적화 분야에서 이런 구조를 “동적 과정(dynamic process)”이라고 불렀던 데서 유래했다고 한다.
0-1. 동적 프로그래밍의 핵심 개념 2가지
1) 중복되는 부분 문제 (Overlapping Subproblems)
큰 문제를 해결하는 과정에서 같은 작은 문제를 여러 번 계산해야 하는 경우가 발생한다.
DP는 이 작은 문제의 결과를 저장해두고 반복 계산을 없애는 방식으로 속도를 크게 개선한다.
2) 최적 부분 구조 (Optimal Substructure)
전체 문제의 최적 해답이 부분 문제의 최적 해답들로 구성될 수 있어야 한다.
즉, 동적 프로그래밍은
1. 중복되는 부분 문제가 존재하고
2. 그 작은 문제들의 최선의 해답으로 큰 문제의 최선 해답을 만들 수 있어야 한다.
대표적인 문제 유형:
- 최단 거리, 최소 비용, 최대 이익, 최소 시간 → 최적화 문제
- 경우의 수 세기, 가능 여부 판별 문제
1. 개념1) 중복되는 부분 문제 - 피보나치 예시
피보나치 수(Fibonacci numbers) 는
첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다.
처음 여섯 항은 각각 1, 1, 2, 3, 5, 8이다. 편의상 0번째 항을 0으로 두기도 한다.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181 …
피보나치 수열은 대표적인 중복 계산 문제가 발생하는 구조다.
F(n) = F(n-1) + F(n-2)
F(0) = 0
F(1) = 1
❌ 단순 재귀 구현의 문제점
int fib(int n)
{
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}이 방식은 중복 계산이 폭발적으로 증가해서, 시간 복잡도가 O(2ⁿ)이 되어버린다.
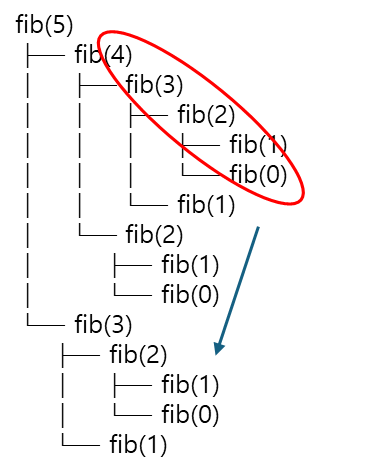
위 방식의 예시 과정을 풀어서 보면

fib(3)과 같은 작은 문제를 여러 번 다시 계산한다.
즉, 이 과정은 부분 문제의 재활용 없이 단순히 "분할만" 하고 있으므로,
DP의 핵심이라고 할 수 있는 최적화 로직은 포함되지 않는다.
1-1. 중복 해결 1: Memoization(메모이제이션) - Top-Down 방식
Memoization = “필요할 때만 계산하고, 계산한 값은 저장한 뒤 재사용한다.” ( 재귀 호출 + 저장 (Memoizing) )
- Top-Down = 큰 문제 → 필요한 작은 문제로 재귀적으로 내려감
- 이미 계산한 값이 있다면 즉시 반환 (중복 제거)
- 중복 제거로 시간 복잡도는 O(N) 수준으로 감소
- 큰 문제를 먼저 호출
- 필요한 작은 문제만 재귀로 내려가면서 계산
- 이미 계산한 작은 문제는 dp[]에서 바로 가져옴
- 중복 계산 없음 → 효율적

| 항목 | 설명 |
| 계산 흐름 | 위 → 아래 |
| 저장 시점 | 계산이 발생하는 순간 저장 |
| 장점 | 필요한 상태만 계산(게으른 계산, Lazy), 구현 직관적 |
| 단점 | 재귀 깊으면 Stack Overflow 위험, 함수 호출 오버헤드 |
개발 시 주의점
- 재귀 깊이가 깊다면 스택 오버플로우 가능 (예: Windows 기본 스택 약 1MB)
- 백준 등 온라인 저지에서는 대체로 큰 문제가 없지만, 실제 서비스 개발에서는 조심해야 한다.
1-2. 중복 해결 2: Tabulation(테뷸레이션) - Bottom-Up 방식
Tabulation = “작은 문제부터 차례대로 모두 계산해 테이블을 채운다.” ( 반복 계산 + 테이블 작성 (Tabulating) )
- Bottom-Up = 가장 작은 상태(dp[0], dp[1])부터 시작 → 마지막 dp[n]까지 순차적으로 모두 계산
- 모든 상태를 미리 계산하므로 재귀 없이 안전
| 항목 | 설명 |
| 계산 흐름 | 아래 → 위 |
| 저장 방식 | 순서대로 테이블 채움 |
| 장점 | StackOverflow 없음, 빠르고 안정적, 캐시 친화적 |
| 단점 | 필요 없는 상태까지 모두 계산해야 함, 메모리 많이 사용 |
주의점
- dp[x][y][z] (3차원) 처럼 상태 차원이 크면 테이블 자체가 생성 불가능
- 그래프/트리 DP 같은 구조는 “일관된 계산 순서”를 만들기 어려워 Bottom-Up이 적합하지 않음
2. 개념2) 최적 부분 구조 - 1로 만들기 문제 예시
최적 부분 구조란,
큰 문제의 최적해가 작은 문제들의 최적해로 구성될 수 있는 구조를 말한다.
대표적인 예로 “정수 N을 1로 만드는 최소 연산 횟수” 문제를 살펴보자.
사용할 수 있는 연산
- N 이 3으로 나누어 떨어지면 == 0 → N = N / 3
- N 이 2로 나누어 떨어지면 == 0 → N = N / 2
- 항상 가능 → N = N - 1
여러 방법으로 1에 도달할 수 있지만, 우리는 연산 횟수가 최소가 되는 경로를 찾는 것이 목표다.
→ 따라서 이 문제는 DP로 해결하기 적합하다.
예) N = 10
여러 경로가 있지만 최소 연산 횟수는 3이다.
| 연산 과정 | 횟수 | 내용 |
| 10 → 9 → 8 → 7 → 6 → 5 → 4 → 2 → 1 | 연산 8번 | -1 계속 비효율 |
| 10 → 9 → 8 → 4 → 2 → 1 | 연산 5번 | 9→8: -1, 8→4: /2, 4→2: /2, 2→1: /2 |
| 10 → 5 → 4 → 2 → 1 | 연산 4번 | 최단은 아님, 하지만 비교적 짧은 경로 |
| 10 → 9 → 3 → 1 | 연산 3번 | -1 , /3 , /3 |
이처럼 각 숫자는 여러 경로로부터 올 수 있으며, 항상 “최소 비용 경로”를 선택하는 구조가 바로 최적 부분 구조이다.
3. 점화식(Recurrence Relation) 이란?
동적 프로그래밍에서 점화식은
현재 상태를 더 작은 상태들의 결과로 표현한 수학적 관계식이다.
즉, 큰 문제를 작은 문제의 해답을 이용해 계산하도록 만드는 구조를 말한다.
예를 들어 피보나치 수열은
F(n) = F(n-1) + F(n-2)라는 점화식으로 정의되며,
이와 같이 “현재 값을 이전 값들을 이용하여 정의하는 방식” 이 바로 DP에서 사용하는 핵심 구조이다.
DP는 이 점화식을 이용해, 테이블을 채워서 전체 문제를 해결한다.
3-1. 점화식 찾는 과정
“정수 N을 1로 만드는 최소 연산 횟수” 문제 를 예시로 점화식을 찾아보도록 하자.
1) dp[i] 의미 정하기
DP를 만들 때 첫 단계는 dp[i]가 무엇을 의미하는지 명확히 정의하는 것이다.
dp[i] = “ 숫자 i를 1로 만들기 위해 필요한 최소 연산 횟수 ”
즉, “i를 1로 만들려면 몇 번의 연산이 필요할까?” 그 답을 저장하는 배열이 dp다.
2) dp[i] 의 계산 방법
i가 바로 이전에 어떤 숫자에서 왔을지 거꾸로 생각해보면 된다.
왜 거꾸로 생각할까?
DP는 “이전 상태에서 현재 상태로 오는 관계”를 이용해서 문제를 푸는 방식이기 때문.
3) i는 ‘딱 세 가지 경우’로만 만들어질 수 있다.
i 를 만들 수 있는 연산은 다음뿐이다:
- (이전 숫자) +1 → i => 즉, i-1에서 왔다
- (이전 숫자) ×2 → i => 즉, i/2에서 왔다 (단, i가 2의 배수일 때만)
- (이전 숫자) ×3 → i => 즉, i/3에서 왔다 (단, i가 3의 배수일 때만)
그래서 i는 이렇게만 올 수 있다:
- i-1 → i
- i/2 → i
- i/3 → i
4) 그래서 dp[i]를 구할 때 해야 할 일은 딱 하나
i로 올 수 있는 세 경로 중에서, 1로 가는 데 가장 적게 걸리는 경로를 선택하면 된다.
예를 들어,
- i-1에서 왔다면 → 필요한 횟수는 dp[i-1] + 1
- i/2에서 왔다면 → 필요한 횟수는 dp[i/2] + 1
- i/3에서 왔다면 → 필요한 횟수는 dp[i/3] + 1
여기서 “+1”은 마지막에 i로 만드는 한 번의 연산 이다.
따라서 dp[i]는 이렇게 계산된다:
dp[i] = 위 세 개 중 가장 작은 값
5) 이게 그대로 점화식이 된다.
// 점화식의 의사 코드
dp[i] = min(
dp[i-1] + 1,
dp[i/2] + 1 (if i % 2 == 0),
dp[i/3] + 1 (if i % 3 == 0)
)| i | dp[i] | 의미 |
| 1 | 0 | 이미 1 → 연산 필요 없음 |
| 2 | 1 | 2 → 1 (1번) |
| 3 | 1 | 3 → 1 (1번) |
| 4 | 2 | 4 → 2 → 1 (2번) |
| 5 | 3 | 5 → 4 → 2 → 1 (3번) |
| 6 | 2 | 6 → 3 → 1 (2번) |
| 9 | 2 | 9 → 3 → 1 (2번) |
| 10 | 3 | 10 → 9 → 3 → 1 (3번) |
즉, dp[10] = 3 라는건, "10을 1로 만들기 위해 최소 3번의 연산이 필요하다" 는 뜻
3-2. 점화식 도출 과정 정리
- dp[i]: i를 1로 만드는 최소 횟수
- i는 세 방법으로만 만들어질 수 있음 → (i-1)+1 , (i/2)*2 , (i/3)*3
- 따라서 dp[i]는 세 가지 경로 중 “최소 횟수 경로 + 1”
4. 정리
Dynamic Programming은 다음 두 가지 조건이 모두 있을 때 강력하게 사용된다.
- 중복되는 부분 문제
- 최적 부분 구조
그리고 이를 구현하는 방식은 두 가지:
| 방식 | Memoization | Tabulation |
| 흐름 | Top-Down | Bottom-Up |
| 특징 | 필요한 것만 계산, 재귀 기반 | 전체 상태 미리 계산, 반복문 기반 |
| 장점 | 직관적, 복잡한 의존관계에 강함 | 빠르고 안정적, 스택오버플로우 없음 |
| 단점 | 재귀 깊이 위험 | 메모리 사용량 높을 수 있음 |
'CS' 카테고리의 다른 글
| [알고리즘] BVH vs Quad/Octree: 차이점, 장단점, 게임엔진 활용 예시 (0) | 2025.12.17 |
|---|---|
| [알고리즘] DP구현: 정수 N을 1로 만드는 최소 연산 횟수 (Top-Down vs Bottom-Up) (0) | 2025.12.15 |
| [알고리즘] BVH : 정적/동적 트리 갱신 (0) | 2025.12.04 |
| [알고리즘] BVH (Bounding Volume Hierarchy) (0) | 2025.11.06 |
| [알고리즘 실습] 멀티 스레드로 TaskGraph 동시성 관리 구현 (WinAPI사용) (0) | 2025.10.31 |
