MOONSUN
[알고리즘] 그래프 : 다익스트라 (Dijkstra) 본문
1. 다익스트라(Dijkstra) 란?
한 지점에서 다른 모든 지점까지 가는 최소 비용(또는 거리)를 찾는 알고리즘
- 그래프(지도) 위에서 가장 짧은 길을 찾는 방법
- ‘가장 가까운 노드부터 확정’ 해나가는 '탐욕적(Greedy) 알고리즘'이라고도 한다.
- 단, 모든 길(간선)의 가중치가 양수(0 이상) 이어야 함
- 음수 가중치가 존재하면, 최단 거리 배열에 이미 확정된 노드 값들이 무효화가 될 수 있어 누적 거리 계산을 전제로 한 알고리즘의 정당성이 붕괴된다.
2. 작동 단계
시작점에서 가장 가까운 노드부터 확정하면서, 주변 노드의 최소 비용을 갱신한다.
1. 출발 노드 설정
- 출발 노드의 비용(distance) = 0
- 나머지 노드의 비용 = ∞ (아직 도달 불가)
2. 비용이 가장 적은 노드 선택
- 방문하지 않은 노드 중 가장 비용이 작은 노드를 고름.
3. 이웃 노드들의 비용 갱신
- 선택한 노드를 기준으로, 그 노드를 거쳐 다른 노드로 가는 비용을 계산.
- 기존보다 짧으면 갱신
4. 해당 노드 확정
- 한 번 선택된 노드는 더 이상 갱신되지 않음.
5. 2~4 반복
- 모든 노드가 확정될 때까지 반복.
2-1. 최단거리를 구해보자
예를 들어, 다음과 같은 그래프가 있다고 하면

- 인접 리스트는 아래와 같이 표현된다.

이제 모든 노드 까지의 최단 거리를 천천히 구해보도록 하자..!

먼저, 아직 도달 불가이기 때문에, 초기값은 모두 무한대로 들어간다.
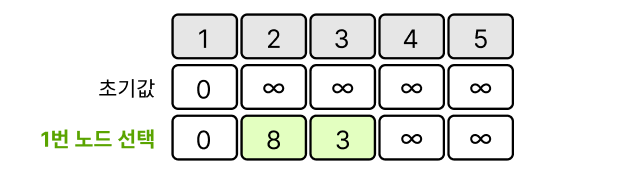
시작 노드는 1번 노드
1번 노드에서 이웃 노드 2번, 3번 노드 까지의 거리를 표시한다.
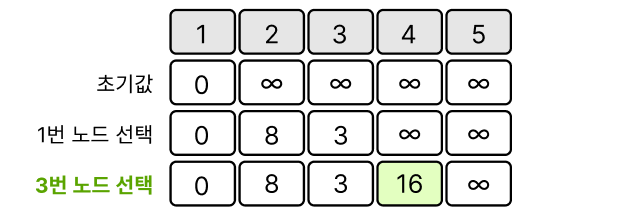
거리가 더 짧은 3번 노드부터 탐색을 시작한다.
3번 노드에서 이웃 노드 4번 노드 까지의 총 거리는 16 (3+13)
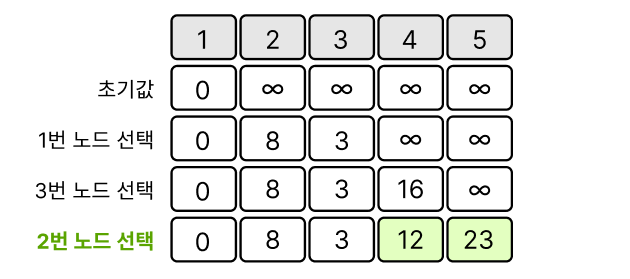
그 다음 으로는 2번 노드의 탐색을 시작한다.
2번 노드에서 이웃 노드 4번, 5번 노드 까지의 총 거리는 각 12 , 23
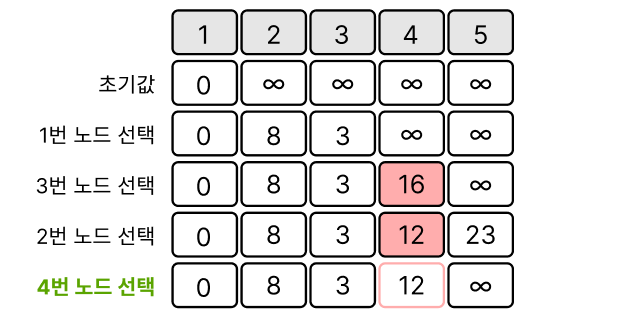
이제 여기에서 시작점 부터 4번 노드까지 가는 최소 거리를 결정 해야한다.
3번 노드를 타고 오는 거리는 16
2번 노드를 타고 오는 거리는 12
더 짧은 거리인 2번 노드 타고 오는 거리 선택.
즉, 1번 → 2번 → 4번 노드 경로
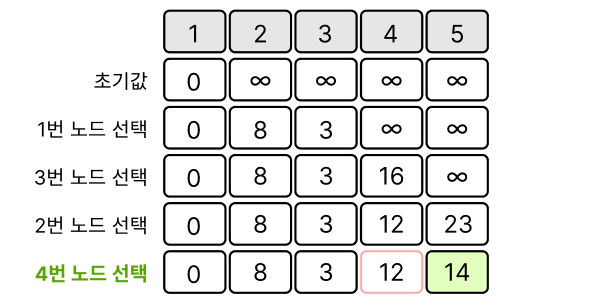
4번 노드의 이웃 노드 5번 노드 까지의 거리는 14
여기에서도 시작점 부터 5번 노드까지 가는 최소 거리를 결정 해야한다.
2번 노드를 타고 오는 거리는 23
4번 노드를 타고 오는 거리는 14
더 짧은 거리인 1번 → 2번 → 4번 → 5번 노드 경로 선택.

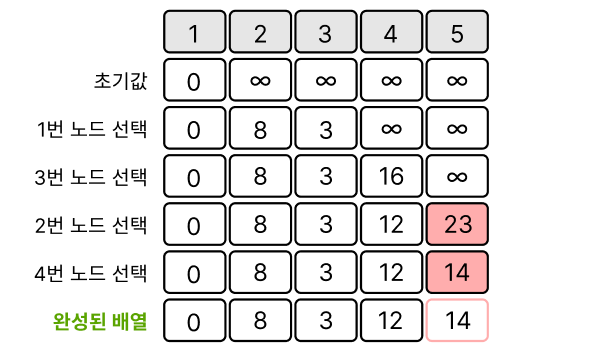
최종 최단 거리 배열은 다음과 같이 완성된다.
3. 경로 추적
어떤 노드의 최단 거리가 갱신될 때마다 ‘이전 노드’를 기록해두면
최종적으로 출발점에서 목적지까지의 경로를 역으로 추적할 수 있다.
위에서 보았던 그래프를 예시로 들면,

최단 경로는 1번 → 2번 → 4번 → 5번 노드의 경로이다.
이 때, 각 노드에 이전 노드(previous node)가 기록 되어 있다면
prev[2] = 1
prev[4] = 2
prev[5] = 4
이전 노드를 따라가면 5번 → 4번 → 2번 → 1번 노드 순서.
즉, 경로를 역으로 추적할 수 있다는 것.
4. 가중치(비용)의 의미
| 가중치(Weight)의 의미 | 실제 예시 | 결과 |
| 도로 거리(km) | 내비게이션 | 가장 짧은 길 |
| 이동 시간(sec) | 교통, 물류 시뮬레이션 | 가장 빠른 경로 |
| 에너지 소모량 | 로봇 이동 | 최소 에너지 경로 |
| 피해량/위험도 | 게임 AI | 가장 안전한 경로 |
| 비용(금액) | 최저가 배송 | 최소 비용 경로 |
즉, “거리”는 단순한 비유이다.
‘비용’, ‘시간’, ‘에너지’, ‘위험도’ 등 어떤 수치든 최소화할 수 있다.
5. DFS와의 차이점
| 구분 | BFS | 다익스트라 |
| 자료구조 | 큐(Queue) | 우선순위 큐 (Priority Queue) |
| 기준 | 탐색 순서(레벨) | 누적 거리(비용) |
| 사용 예 | 모든 간선의 비용이 동일할 때 | 가중치가 다를 때 |
즉,
BFS는 칸 수가 같을 때 최단거리,
다익스트라는 가중치(비용)이 다를 때 최단거리.
'CS' 카테고리의 다른 글
| [알고리즘] 그래프 : A*(asterisk) 알고리즘 (1) | 2025.10.23 |
|---|---|
| [백준 C++] 11779번: 최소비용 구하기2 (0) | 2025.10.20 |
| [자료구조] 그래프(Graph) 와 위상 정렬(Topological Sort) (0) | 2025.10.01 |
| [알고리즘] 효율적인 '자료구조 기반' 정렬(N log₂N): 힙 정렬(Heap Sort) (0) | 2025.09.26 |
| [알고리즘] 효율적인 '분할 정복' 정렬(N log₂N): 퀵 정렬(Quick Sort), 병합 정렬(Merge Sort) (0) | 2025.09.26 |
