MOONSUN
[알고리즘] DP 설계의 출발점: 폭발 관찰과 상태 압축 본문
이전 글에서도 그렇고, Dynamic Programming 문제를 해결할 때의 핵심은 "점화식"을 찾는 것이었다.
하지만 DP 문제를 풀다 보면
점화식은 맞는 것 같은데 시간 초과가 나거나, 배열 크기를 키우면 메모리가 터지고,
경우의 수를 세려다 숫자가 감당할 수 없이 커지는 문제를 맞이하게 된다.
문제는 점화식이 아니라, 불필요한 정보까지 상태로 들고 가고 있다는 점이다.
이번 글에서는 “모든 경우를 그대로 저장하면 왜 안 되는지”를 출발점으로,
미래 계산에 꼭 필요한 정보만 남기는 상태 압축과 그 상태에서 자연스럽게 점화식을 도출하는 과정을 정리해보고자 한다.
1. 1차원 DP와 2차원 DP
- 1차원 DP : 결과를 정의하는 데 정보가 하나면 충분한 경우
- 2차원 DP : 결과를 정의하려면 두 가지 정보가 필요한 경우
1차원 DP는 하나의 상태만 기록하면 충분한 문제였다.
하지만 어떤 문제는 결과를 정의하기 위해 두 개의 정보가 필요하고, 이때 2차원 DP를 사용한다.
1-1. 2차원 DP 예시 : 파스칼의 삼각형
대표적인 예시로 파스칼의 삼각형이 있다.
파스칼의 삼각형은 이항계수를 삼각형 형태로 배열한 것으로, 다음과 같은 방법으로 만들 수 있다

- N번째 행에는 N개의 수가 있다.
- 첫 번째 행은 1이다.
- 두 번째 행부터, 각 행의 양 끝의 값은 1이고, 나머지 수의 값은 바로 위 행의 인접한 두 수의 합이다.
예를 들어, n=3이면 3번째 행의 2번째 수는 위 행의 인접한 두 수 (1과 1)을 더해서 만든다.
n=6일 때, 파스칼 삼각형의 6번째 행의 10은 5번째 행의 인접한 두 수(4와 6)을 더해서 구한다.
- dp[n][k] : n번째 행의 k번째 수
- 위에서 내려오며 계산됨
점화식은 다음과 같다.
dp[n][k] = dp[n-1][k-1] + dp[n-1][k]
해당 문제는 상태도 작고 (n ≤ 30), 값도 크지 않아서 → 단순 2차원 DP로 충분히 해결 가능하다.
DP는 항상 이렇게 점화식만 찾으면 끝일까?
→ 아님. 진짜 어려운 문제는 "상태를 어떻게 정의하느냐"
2. 상태 압축(State Compression)이란?
미래 계산에 영향을 주지 않는 정보는 버리고, 꼭 필요한 정보만 상태로 남긴다.
문제에서 발생하는 모든 경우의 정보를 그대로 다루는 대신,
이후의 계산과 결과에 영향을 주는 정보만을 상태로 남겨서 점화식과 전이로 표현 가능한 형태로 추상화 함으로써,
조합 폭발을 억제하고 문제를 성립 가능한 상태 공간으로 축소하는 것
2-1. 전이 (Transition)
"한 상태에서 다음 상태로 이동할 수 있는 규칙"
이전 상태의 결과가 다음 상태의 점화식 계산에 사용되는 관계를 의미
점화식이란 결국 → 이 상태에서 다음 상태를 어떻게 만들까?
2-2. 조합 폭발(Combinatorial Explosion) 문제
하지만, 문제를 있는 그대로 다루면:
- 경우의 수가 기하급수적으로 증가
- 메모리 초과
- 시간 초과
- 자료형 한계 초과
의 문제를 만날 수 있다. 이걸 "조합 폭발" 이라고 한다.
이런 조합 폭발의 문제를 막기 위해서 상태 압축을 해야한다.
3. 폭발이 발생하는 예: 등굣길 문제
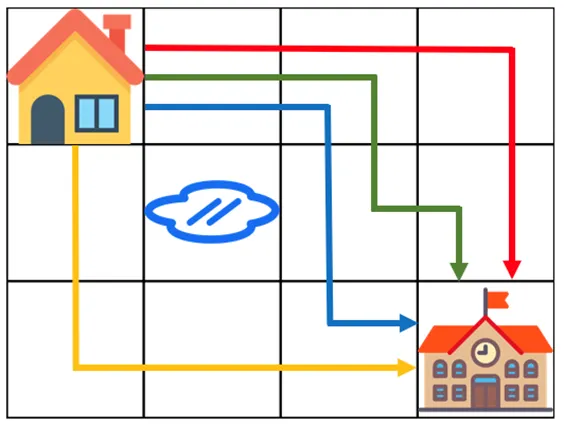
문제 상황 : 가로 4, 세로 3 크기의 격자에서 (0,0) 집에서 (3,2) 학교까지 이동한다.
- 이동은 Right(R) 또는 Down(D) 만 가능하다.
- 필수 이동 횟수가 정해진다.
- Right 이동: 3번
- Down 이동: 2번
- 총 이동 횟수: 5번
- 5개의 자리 중에서 R이 들어갈 3개의 자리를 선택만 하면, 나머지 자리는 자동으로 D가 채워지게 된다.
3-1. 잘못된 접근 : 모든 경로 나열

RRRDD RRDRD RRDDR RDRRD RDRDR RDDRR
DRRRD DRRDR DRDRR DDRRR
이런 식으로, 모든 경로를 나열 한다면?
격자가 커질 수록
- 모든 경로 저장 X
- 모든 순열 계산 X
결국, 구조 폭발 발생
3-2. 관찰을 통한 압축
조금 생각해보면, 우리는 사실
- “어떤 순서로 왔는지” 가 아니라
- “지금 어느 칸에 있는지” 만 필요하다는걸 알 수 있다.
그러면 상태를 이렇게 정의할 수 있다.
dp[i][j] = (i, j)까지 오는 경로의 수
즉, 상태 압축을 통해서 아래와 같이 전이 설계할 수 있다.
dp[i][j] = dp[i-1][j] + dp[i][j-1]과거의 모든 경로를 저장하지 않고, 결과에 필요한 정보만 남긴다.
4. 또 다른 압축 방법: 값 압축 (MOD 연산)
(여러 압축 방법에 대해서는 아래에서 따로 설명할 예정)
정답 조건이 실제 경우의 수를 찾는 것이 아니라서, 실제 값 자체가 필요 없는 경우
즉, 다음과 같은 상황
- 경로 수가 너무 큼
- 실제 값 자체는 필요 없음
- “어떤 수로 나눈 나머지”만 요구
4-1. 핵심 성질

(a + b) % M = ((a % M) + (b % M)) % M
중간에 나눠도 최종 결과는 동일하다..!!
4-2. DP 점화식에 적용
점화식에 적용하면 아래와 같이 된다.
dp[i][j] = (dp[i-1][j] + dp[i][j-1]) % MOD
- 값이 커지지 않고, 자료형이 안전해진다.
- 정확한 값 → “의미 있는 나머지 값” 으로 상태 압축된다.
5. 상태 압축이 필요한 폭발의 종류
| 폭발 종류 | 예시 | 해결 방법 |
| 구조 폭발 | 모든 경로, 모든 순열 | 상태 압축 |
| 값 폭발 | 경로 수, 조합 수 | MOD, 의미 축소 |
| 상태 공간 폭발 | 차원 너무 큼 | 상태 의미 재정의, 대칭성 활용 |
DP에서 말하는 압축은 하나의 기법이 아니라,
문제 해결에 불필요한 정보를 제거하는 모든 방법을 포괄하는 개념이다.
구조를 줄이는 상태 압축, 값의 크기를 줄이는 MOD 연산, 상태 의미를 재정의하는 추상화 모두 압축의 형태이다.
6. DP 설계를 위한 3가지 질문
폭발을 관찰하고, 정보를 압축하여 그 압축된 세계에서 점화식이 올바르게 정의 되도록 전이를 설계해야 한다
DP 문제를 만났을 때, 아래 질문을 순서대로 던져보면 큰 도움이 된다.
6-1. 모든 경우를 그대로 저장하면 왜 안 되지?
- 어디서 폭발하는가?
- 무엇을 버려야 하는가?
버릴 정보를 찾는 단계 (압축 대상 찾기)
6-2. 미래 계산에 정말 필요한 정보는 무엇인가?
- 결과를 만들기 위해 꼭 필요한 정보는?
- 나머지는 없어도 되는가?
상태 정의 단계 (무엇만 남길 것인지)
6-3. 이 상태만으로 다음 상태를 만들 수 있는가?
- 이 상태에서 전이가 가능한가?
- 이전 상태를 다시 보지 않아도 되는가?
전이 가능성 검증 단계
DP는 점화식을 먼저 세우는 게 아니라,
폭발을 관찰하고 → 상태를 압축하고 → 그 상태에서 가능한 전이를 설계하는 과정이다.
이 3개가 연결되면 자연스럽게 점화식을 구할 수 있다.
'CS' 카테고리의 다른 글
| [알고리즘] BVH vs Quad/Octree: 차이점, 장단점, 게임엔진 활용 예시 (0) | 2025.12.17 |
|---|---|
| [알고리즘] DP구현: 정수 N을 1로 만드는 최소 연산 횟수 (Top-Down vs Bottom-Up) (0) | 2025.12.15 |
| [알고리즘] Dynamic Programming(DP:동적 프로그래밍)이란? (0) | 2025.12.12 |
| [알고리즘] BVH : 정적/동적 트리 갱신 (0) | 2025.12.04 |
| [알고리즘] BVH (Bounding Volume Hierarchy) (0) | 2025.11.06 |
