MOONSUN
[게임 수학] 행렬 연산의 특징 : 비가환성, 역행렬, 전치(Transpose) 등.. 본문
그래픽스에서 필수 요소인 행렬 연산의 특징들에 대해 간단하게 알아보자.
1. 곱셈의 비가환성 ( 순서 중요 )
행렬 곱셈은 두 행렬을 결합하여 하나의 변환을 만드는 연산이다.

즉, “먼저 이동 후 회전”과 “먼저 회전 후 이동”은 다른 결과를 만든다.
1-1. 행렬 곱셈 계산 방법
참고로 행렬의 곱셈 방법은 다음과 같음.

- 첫 번째 행렬의 각 행과 두 번째 행렬의 각 열을 내적(dot product)하여 계산
- 이 연산이 정의되기 위해서는 첫 번째 행렬의 열 개수가 두 번째 행렬의 행 개수와 같아야 함
1-2. 비가환성 예시
- T = x축으로 +5 이동
- R = 원점을 기준으로 90° 회전
- 위 내용을 어떤 점 v=(1,0)에 적용해보면.
- RTv (먼저 이동 후 회전) : (1,0) → (6,0) [이동] → (0,6) [회전]
- 점이 이동하고 난 뒤, 그 위치를 기준으로 회전
- TRv (먼저 회전 후 이동) : (1,0) → (0,1) [회전] → (5,1) [이동]
- 점이 먼저 회전하고 난 뒤, 회전된 방향으로 이동
- RTv (먼저 이동 후 회전) : (1,0) → (6,0) [이동] → (0,6) [회전]
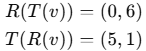

결과가 다름 -> 행렬 곱은 순서가 바뀌면 달라진다.
2. 역행렬 (Inverse)
행렬 : "변환" 이라는 의미
역행렬 : 그 "변환을 원래대로 되돌리는" 의미

정의

역행렬 (순서 반대)
여러 변환을 합쳤다면 되돌릴 때 순서를 거꾸로 해야 한다.
2-1. 역행렬 예시
- 변환 : 스케일 후 회전

- 역변환 : 회전 취소 후 스케일 취소

3. 전치 (Transpose)
전치 행렬을 행(row)과 열(column)을 뒤집은 행렬 이다.
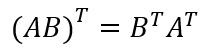

역시 곱의 순서가 뒤집힌다.
3-1. 회전 행렬과 전치
회전 행렬 R의 특징은 직교행렬(orthogonal matrix)이라는 점
- 직교행렬 = 행렬의 열벡터(또는 행벡터)들이 서로 직각이고, 모두 길이가 1인 벡터로 이루어진 행렬

즉,
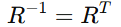
회전의 역행렬은 전치와 같다.
이건 그래픽스에서 아주 중요한 성질!!!
3-2. 벡터 내적과 행렬 전치
3-2-1. 벡터의 표현 방식
선형대수에서는 벡터를 보통 열벡터(column vector) 로 쓴다.

이렇게 세로(열) 로 표현하는 게 기본
열벡터는 n×1 행렬이라고 보면 됨.
3-2-2. 내적의 행렬 표현
- 내적은 다음과 같았다. (단순히 원소끼리 곱하고 더한 값) :

그런데, 행렬 곱셉을 하려면 첫 번째 행렬의 열 개수와 두 번째 행렬의 행 개수가 맞아야 하기 때문에,
그냥 u⋅v 는 (3×1)×(3×1) 이라서 곱할 수 없음.
그래서 u를 전치(Transpose) 해서 가로(행)으로 바꿔준다!!
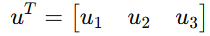
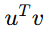
는 (1×3) × (3×1) = (1×1) = 1
즉, 스칼라가 된다. (내적의 값도 스칼라로 나옴)
실제 계산은 다음과 같다.
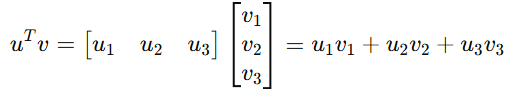
바로 내적 !!!!
3-2-3. 요약
- 내적 = 원소끼리 곱하고 합.
- 행렬 곱으로 표현하려면, 벡터 하나를 전치해서 “행 × 열” 꼴로 만들어야 함.
- 그래서 다음과 같이 표준 공식처럼 씀:

즉, “전치”는 내적을 행렬 곱으로 표현하기 위한 ‘모양 맞추기 도구’라고 이해할 수 있다.
4. 결합법칙
행렬 곱에서는 곱의 순서를 바꾸는 건 안 되지만, 괄호 묶는 방식(결합 법칙)은 바꿀 수 있다.

결과는 항상 동일한 행렬.
4-1. 그래픽스에서 의미
- 즉, 한 점 v에 여러 변환을 적용 해야할 때,
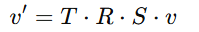
- "3개의 변환 행렬을 미리 하나로 합쳐놓고" 정점 v에 한 번만 곱하면 됨.

(계산 횟수가 줄어들고, 성능 최적화 되는 장점)
5. 분배법칙
한 행렬을 여러 행렬/벡터에 동시에 곱할 수 있다.

5-1. 그래픽스에서 의미
- 여러 점이나 벡터 v1,v2,v3 에 같은 변환 A를 적용할 때

- 즉, 변환을 벡터마다 따로 적용해도 되고,
- 먼저 합쳐서 한 번에 적용해도 결과가 동일하다.
(역시, 계산 횟수가 줄어들고, 성능 최적화 되는 장점)
'D3D' 카테고리의 다른 글
| [게임 수학] 반사 벡터(Reflection Vector)와 투영 벡터(Projection Vector)) (0) | 2025.09.23 |
|---|---|
| [D3D 이론] 빛(Lighting) 모델 : Phong, Blinn-Phong 와 수식 의미 (0) | 2025.09.22 |
| [게임 수학] 벡터의 내적(Dot product) 과 외적(Cross product) (0) | 2025.09.18 |
| [그래픽스] 빛(Lighting) 모델 : Lambertian Shading (램버트 조명 모델) (0) | 2025.09.15 |
| [D3D] 상수버퍼(Constant Buffer) 와 HLSL 정렬규칙 (0) | 2025.09.10 |

