MOONSUN
[게임 수학] 반사 벡터(Reflection Vector)와 투영 벡터(Projection Vector)) 본문
앞 글에서 라이팅 모델들에 대해 알아봤는데, 반사 벡터 라는 개념이 언급되었었다.
이 글에서는 반사 벡터와 유도 수식을 알아보도록 하자.
1. 반사 벡터 (Reflection Vector)
말 그대로 반사 벡터 란,
어떤 물체 표면에 빛(또는 입사 벡터)가 들어왔을 때, 그 표면에서 거울처럼 튕겨져 나가는 방향을 나타내는 벡터를 말한다.
2. 투영 벡터를 구해보자.
반사 벡터를 구하려면, 먼저 투영 벡터를 구할 수 있어야 한다.
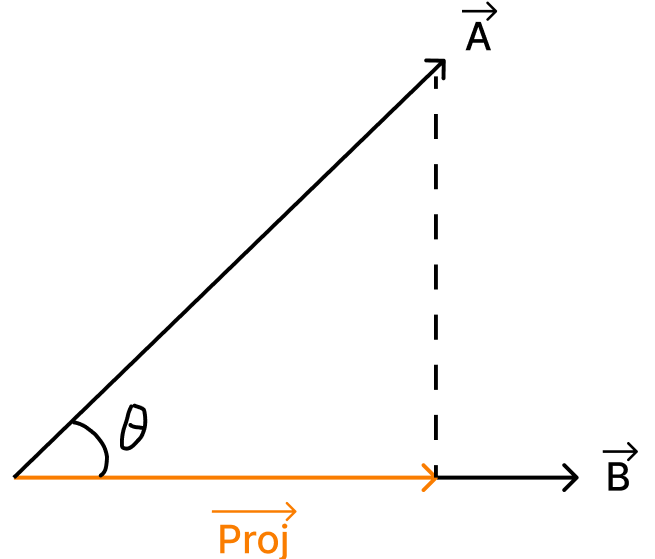
우리가 원하는 건 A를 방향으로 벡터 투영하는 것.
( B는 크기가 1인 방향 단위벡터라고 가정한다. )
2-1. 투영 크기

cosθ = 밑면 / 빗면 이다.
- 위의 Fig.1 그림에서, 밑면 = Prog(A) 이고, 빗면 = |A| 이다.
- cosθ = Prog(A) / |A| 이므로
- 위와 같은 식, Prog(A) = |A| cosθ 가 된다.
즉, A를 B의 위로 내렸을 때, 그 길이는 |A| cosθ 가 된다.
2-2. 내적 사용

내적 공식은 위와 같았다.
그런데, 우리의 B는 크기가 1인 방향 단위벡터 이기 때문에,
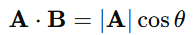
위와 같은 식이 된다.
즉, 내적 값 자체가 투영 길이가 된다는 것.
2-3. 대입 (투영 길이)
간단하다, 2-1 과 2-2를 합쳐보자.
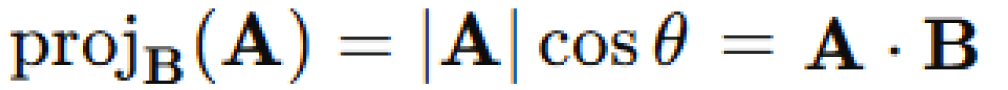

이미 2-2에서 내적 값 자체가 투영 길이가 된다는 것을 알게 되었기 때문에
필요 없는 과정이기도 하지만, 이해를 위해 식을 다시 정리해봤다.
2-4. 방향 부여
방향은 B와 같아야 하므로, 방향을 곱해준다.
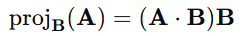
2-5. 결론
즉, (B가 단위벡터일 때) 투영 공식은 다음과 같다.
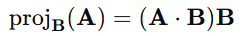
이렇게 구한 투영 공식은 반사 벡터를 구하는 과정에서 사용될 것이다.
3. 반사 벡터를 구해보자.
입사벡터 P와 법선벡터 n이 주어졌을 때, 반사벡터 R은 어떻게 구할 수 있을까?
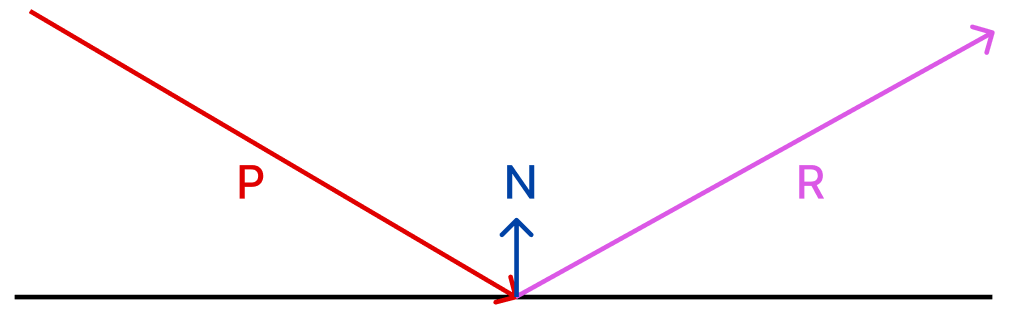
3-1. P의 역벡터를 N에 투영(Projection)시킨다.

위에서 구했던 투영 공식은 N(-PㆍN)
3-2. P를 원점으로 이동시키고 n(-Pㆍn)을 더하면 P1이 나온다.
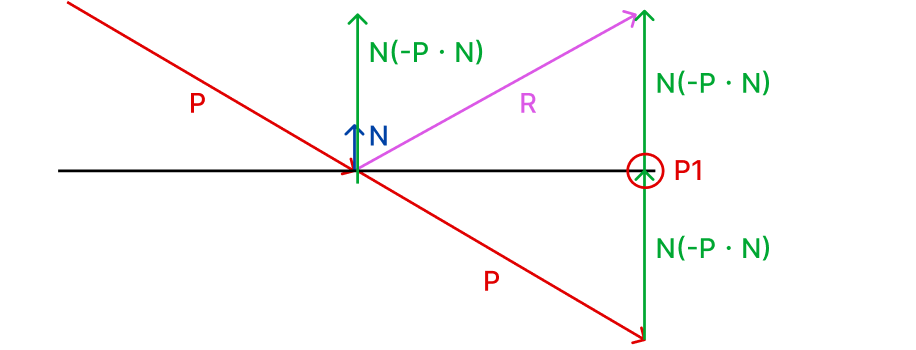
3-3. 한번 더 더하면 반사벡터 R을 구할 수 있다.

즉, 반사벡터 R = P + 2N(-PㆍN) 이다.

'D3D' 카테고리의 다른 글
| [D3D] Direct3D 11 렌더링 파이프라인 주요 객체 (0) | 2025.09.29 |
|---|---|
| [D3D] Vertex Shader에서 이루어지는 월드/뷰/투영 변환 (0) | 2025.09.24 |
| [D3D 이론] 빛(Lighting) 모델 : Phong, Blinn-Phong 와 수식 의미 (0) | 2025.09.22 |
| [게임 수학] 행렬 연산의 특징 : 비가환성, 역행렬, 전치(Transpose) 등.. (0) | 2025.09.19 |
| [게임 수학] 벡터의 내적(Dot product) 과 외적(Cross product) (0) | 2025.09.18 |
