MOONSUN
[D3D 이론] 빛(Lighting) 모델 : Phong, Blinn-Phong 와 수식 의미 본문
이전에는 게임 그래픽스의 빛 계산(Lighting) 모델로 램버트(Lambert) 모델에 대해 알아봤었다.
램버트 모델을 소개하면서 다른 모델들에 대해서도 간단 언급했었는데,
이번에는 나머지 모델인 Phong과 Blinn-Phong에 대해 알아보고자 한다.
들어가기에 앞서, 간단 요약해보면 다음과 같다.
| 모델 | 특징 | 현실감 정도 |
| Lambert | 확산광만, 하이라이트 없음 | 낮음 (무광 느낌, 매트 느낌) |
| Phong | 확산광 + 정반사 하이라이트 + 환경광(Ambient) | 중간 이하 (광택 표현 가능하지만 비물리적) |
| Blinn-Phong | 확산 + 정반사 하이라이트 (Half Vector 사용, 부드럽고 빠름) + 환경광 | 중간 (플라스틱/금속 느낌, 옛날 게임 표준) |
| PBR | 물리 기반, 금속도/거칠기/환경광 포함 | 높음 (현실적 재질 표현, 현대 엔진 표준) |
즉, Lambert → Phong → Blinn-Phong → PBR 순으로 점점 복잡하고 현실감이 높아진다.
1. Phong Shading (1975)
GPU 성능이 좋지 않았던 과거의 Legacy Shading 모델
픽셀의 최종 색상은 환경(ambient)광+ 확산(diffuse)광+ 정반사(specular)광의 합으로 결정한다.
- 구성 요소: Ambient + Diffuse + Specular
- Ambient: 씬 전체의 최소 밝기
- Diffuse: 표면에 닿은 빛이 균일하게 퍼짐
- Specular: 반사된 빛(거울 같은 하이라이트)
1-1. 환경광 (Ambient)
- 씬 전체에 균일하게 퍼져 있는 최소 밝기
- 실제로는 "간접광(Indirect light)"을 단순화한 개념
- 그림자가 져도 완전히 까맣지 않은 이유
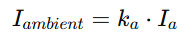

1-2. 확산광 (diffuse)
- 빛이 표면에 닿으면 모든 방향으로 퍼져 나가는 빛
- 표면이 빛을 얼마나 정면으로 받는지에 따라 세기가 달라짐 (법선과 광원 방향 각도에 의존)


1-2-1. Phong의 확산광(diffuse)
“빛이 표면에 닿으면, 표면 위에서 바로 모든 방향으로 고르게 퍼져나간다.”고 단순하게 정의

- 즉, 표면에 빛이 닿자마자 산란(reflection) 되는 것으로 취급.
- 표면 재질이 어떤 구조인지, 내부에서 무슨 일이 일어나는지는 고려하지 않기 때문에,
- 나무, 돌, 플라스틱, 종이 → 다 똑같은 방식으로 확산광을 계산한다.
“빛이 표면에서 바로 튕김” (재질 무시, 단순화된 가정)
1-2-2. PBR의 확산광(diffuse)
현실 세계에서는 빛이 표면에 닿으면 바로 튕기지 않고, 표면 내부로 조금 들어간다.

- 재질의 두께, 색, 밀도에 따라 빛의 퍼짐이 달라짐
“빛이 재질 내부로 들어가 산란 후 나옴” (재질 특성 반영)
1-3. 정반사광 (Specular)
- 거울처럼 반짝이는 하이라이트
- 입사각 = 반사각 조건을 만족할 때 카메라 쪽으로 강한 빛이 보임
- 광택이 강할수록(높은 shininess 값) 좁고 선명한 하이라이트
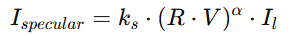


2. Blinn-Phong Shading (1977)
개선된 Phong 모델
정반사광(specular) 계산에서, 반사벡터 R 대신 -> Half Vector(H) 를 사용
- Half Vector (H)
- = (빛 방향 L + 카메라 방향 V) / |L+V|
- 반사 벡터 계산을 줄이기 위해 근사치(Half Vector: H) 를 사용해 계산 효율이 좋아지고,
- 하이라이트가 더 넓고 부드럽게 표현됨
3. Phong과 Blinn-Phong의 정반사(Specular) 계산
- Phong : 반사 벡터 (R) 사용
- Blinn-Phong : 빛과 뷰 사이 중간 벡터 (H) 사용
3-1. Phong의 정반사 항
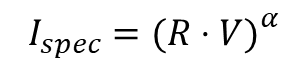

- 𝑅 : 입사광 𝐿을 법선 𝑁기준으로 반사시킨 벡터
- 𝑉 : 뷰(카메라) 방향
- 𝛼 : shininess (광택 지수)
3-2. Blinn-Phong의 정반사 항


- 𝐻 = (𝐿+𝑉) / (∣𝐿+𝑉∣) : Half vector (빛과 뷰 사이 중간 벡터)
- 𝑁 : 표면 법선
- 𝛼 : shininess
4. Phong과 Blinn-Phong 수식
두 모델의 최종 수식은 다음과 같다.
- Phong 모델

- Blinn-Phong 모델

4-1. 의미

1. 첫 번째 항 : 환경광(Ambient) → 씬 전체에 균일한 최소 밝기

2. 두 번째 항 : 확산광(Diffuse) → 표면이 광원 방향에 얼마나 노출되었는지

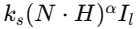
3. 세 번째 항 : 정반사광(Specular) → 하이라이트
즉, 최종 픽셀 색상 = Ambient + Diffuse + Specular 구조의 수식 표현이다.
4-2. 차이

Phong : 반사 벡터 계산 필요, 하이라이트 좁고 날카로움
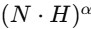
Blinn-Phong : 반사벡터 계산 없이 Half Vector 사용, 하이라이트 넓고 부드러움
5. 요약
Phong 모델은 환경광+ 확산광+ 정반사광의 합으로 픽셀의 최종 색상을 결정하는 모델이고,
Blinn-Phong 모델은 Phong 모델을 더 효율적으로 연산 하는 모델이다.
라이팅 모델에 대해 설명하다보니, "반사 벡터 (reflection vector)"를 언급하게 되었는데,
이후 글에서는 반사 벡터에 대해서 정리해보고자 한다..!
'D3D' 카테고리의 다른 글
| [D3D] Vertex Shader에서 이루어지는 월드/뷰/투영 변환 (0) | 2025.09.24 |
|---|---|
| [게임 수학] 반사 벡터(Reflection Vector)와 투영 벡터(Projection Vector)) (0) | 2025.09.23 |
| [게임 수학] 행렬 연산의 특징 : 비가환성, 역행렬, 전치(Transpose) 등.. (0) | 2025.09.19 |
| [게임 수학] 벡터의 내적(Dot product) 과 외적(Cross product) (0) | 2025.09.18 |
| [그래픽스] 빛(Lighting) 모델 : Lambertian Shading (램버트 조명 모델) (0) | 2025.09.15 |
